函数式编程

JavaScript 并非函数式编程语言，但在 JavaScript 中可以应用函数式编程技术。下面会着重介绍 JavaScript 中的函数式编程技术，一起来体会下 JavaScript 函数的强大吧。

使用函数处理数组

假设有一个数组，数组元素都是数字，我们想要计算这些元素的平均值和标准差，如使用非函数式编程风格，代码会是这样：

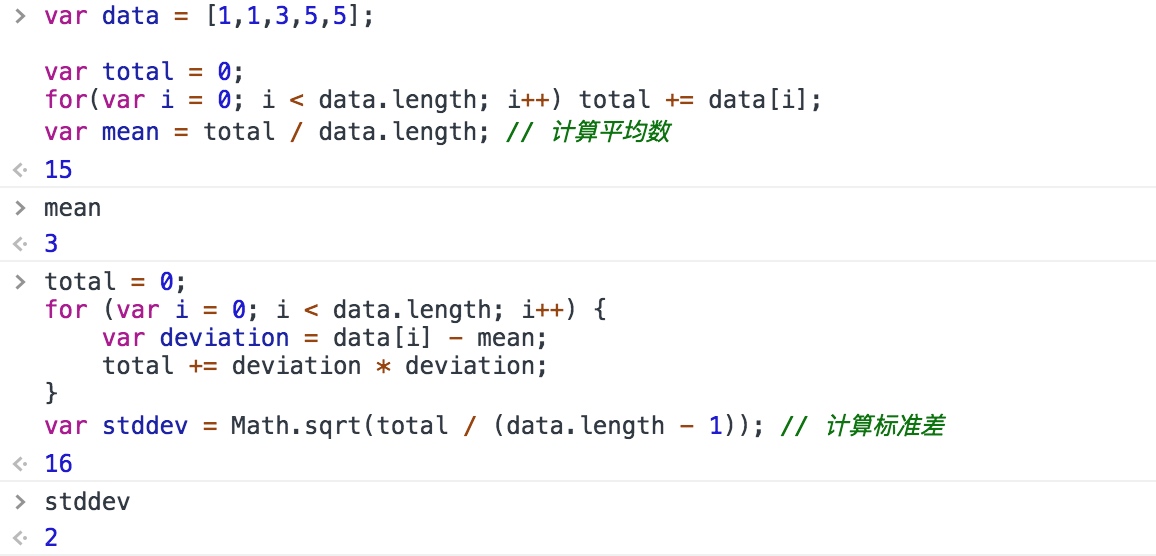
可以使用数组函数 map() 和 reduce() 实现同样的计算，这种实现更加简洁，复用性更好：

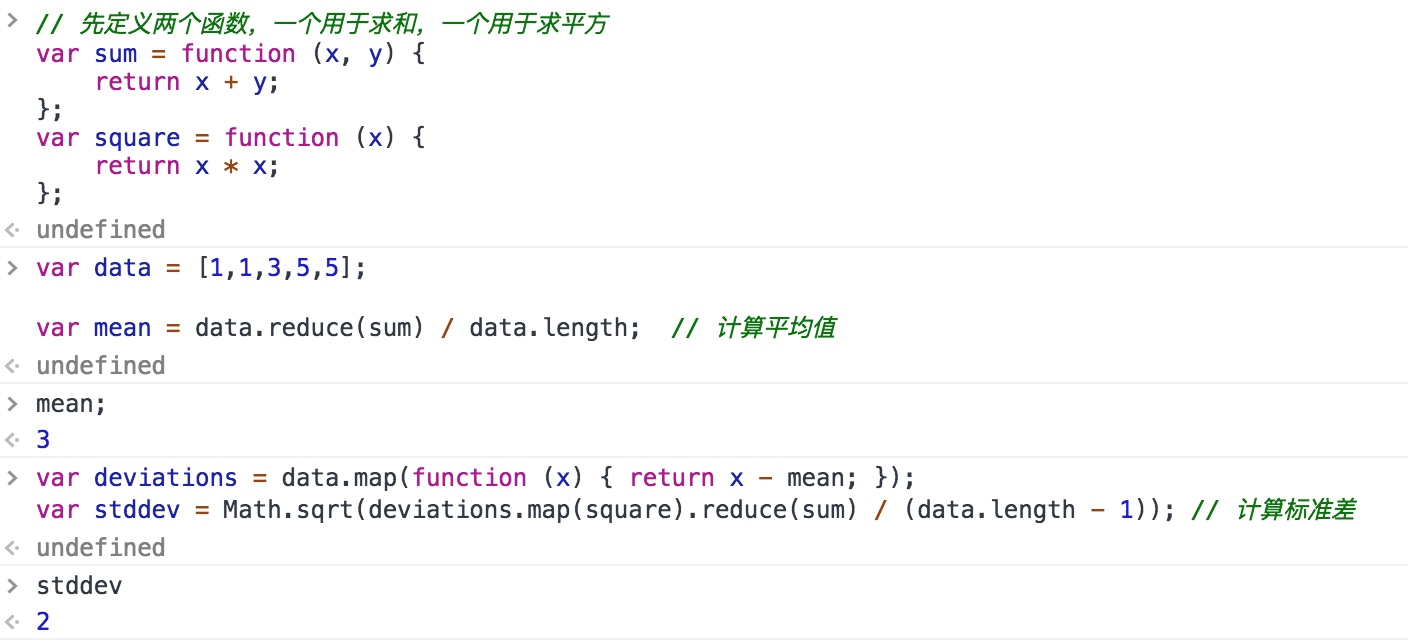
高阶函数

所谓高阶函数（higher-order function），就是操作函数的函数，它接收一个或多个函数作为参数，并返回一个新函数：

通过这种方式可以快捷定义判断传入数据是否是奇数的函数。

下面再看一个例子，通过高阶函数定义的新函数将一个数组映射到另一个使用这个函数的数组上：

下面看一个更常见的例子，它接收两个函数 f() 和 g()，并返回一个新的函数用于计算 f(g())：

不完全函数

把一次完整的函数调用拆成多次函数调用，每次传入的实参都是完整实参的一部分，每个拆分开的函数叫做不完全参数，每次函数调用叫做不完全调用，这种函数调用的特点是每次调用都返回一个函数，直到得到最终运行结果为止。举个例子，将对函数 f(1,2,3,4,5,6) 的调用修改成等价的 f(1,2)(3,4)(5,6)，后者包括三次调用，和每次调用相关的函数就是「不完全函数」。

下面看一个具体的例子：

// 编写一个工具函数将类数组对象转化为真正的数组
function array(a, n) {
  return Array.prototype.slice.call(a, n || 0);
}

// 这个不完全函数实现参数传递至左侧
function partial_left(f /*,...*/) {
  var args = arguments;   // 保存外部实参数组
  return function () {
    var a = array(args, 1);  // 定义一个实参列表，将外部参数排除第一个参数（函数f）后作为初始值
    a = a.concat(array(arguments)); // 然后将所有内部参数添加到这个实参列表
    return f.apply(this, a);  // 最后基于这个实参列表调用函数 f()
  }
}

// 这个不完全函数实现参数传递至右侧
function partial_right(f /*,...*/) {
  var args = arguments;
  return function () {
    var a = array(arguments);  // 定义一个实参列表，将内部参数作为初始值
    a = a.concat(array(args, 1));  // 排除外部参数第一个参数（函数f()）后将其余参数添加到实参列表
    return f.apply(this, a);  // 最后基于这个实参列表调用函数 f()
  }
}

// 这个不完全函数的实参被用作模板，实参列表中的undefined值被内部参数填充
function partial(f /*,...*/) {
  var args = arguments;
  return function () {
    var a = array(args, 1); // 定义一个实参列表，将外部参数排除第一个参数（函数f）后作为初始值
    var i = 0, j = 0;
    // 遍历 args 用内部参数填充外部参数 undefined 值
    for (; i < a.length; i++) {
      if (a[i] === undefined)
        a[i] = arguments[j++];
    }
    // 现在将剩下的内部参数都放进去
    a = a.concat(array(arguments, j));
    return f.apply(this, a);
  }
}

var f = function (x, y, z) {
  return x * (y - z);
};

以下是对上述函数 f 的不完全调用，注意其区别：

利用这种不完全函数的编程技巧，可以编写一些有意思的代码，利用已有的函数来定义新函数：

我们还可以将高阶函数和不完全函数整合到一起来重新定义 not 函数：

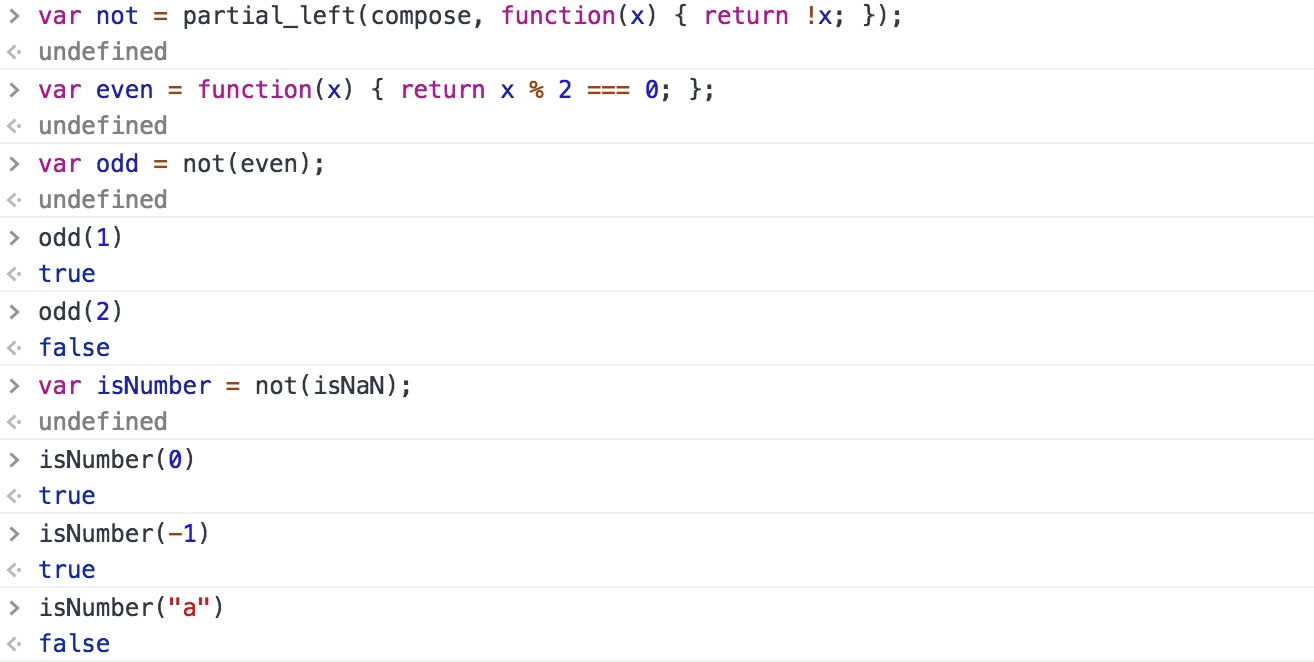
记忆

我们在前面定义过一个阶乘函数，它可以将上次计算结果保存起来，在函数式编程中，这种缓存技巧叫做「记忆」，下面的代码展示了一个高阶函数，memorize() 接收一个函数作为实参，并返回带有记忆能力的函数：

这是一种以空间复杂度换取时间复杂度的编程技巧，在客户端 JavaScript 代码执行时间成为瓶颈时，可以考虑使用该技巧对代码进行重构，比如递归函数：