Leetcode基础刷题之PHP解析(130. Surrounded Regions）

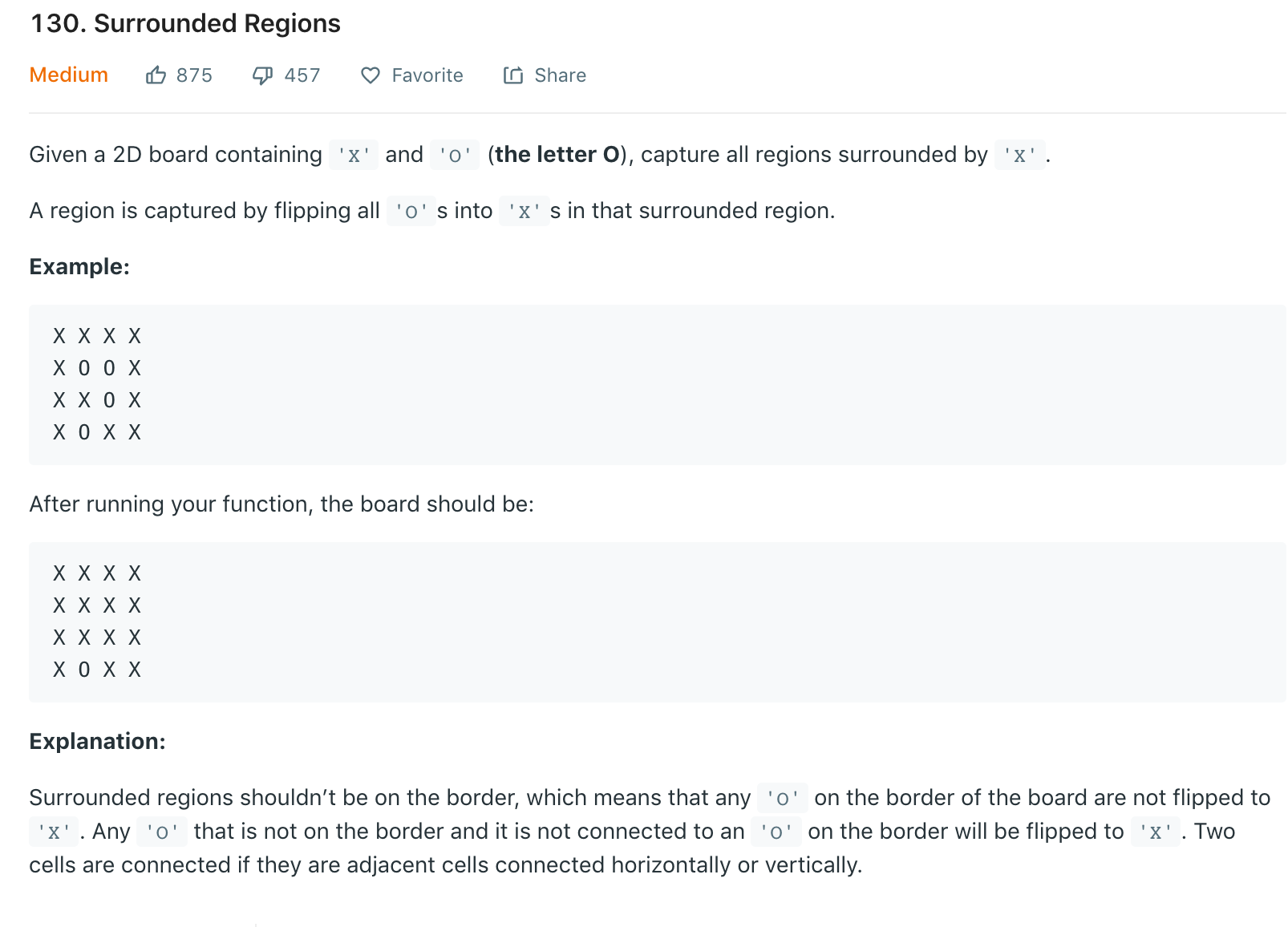
题目描述

这道题很有意思。给定一个2D?我把它理解成二维数组只包含X和O的二维数组，把所有被包围的O全转换成X，下面有说明，如果O是存在在边界上的，那么不需要转换，也就是矩阵的四条边的位置是不需要转换的。

题目分析

一种很巧的解法就是我们可以先把四条边界上是O的值转换成其他的字符(Y)，用来区别被包围的O,这样的话剩下循环遍历到的O都是被包围的，可以直接转换成X，然后再把之前四条边转换成Y的数重新转换成O。所以我们第一步递归四条边界的值，找出O先暂时转换为Y，第二步再遍历一次二维数组把O的值转换成X，把Y的值转换成O，搞定.

代码实现

class Solution {

    /**
     * @param String[][] $board
     * @return NULL
     */
    function solve(&$board) {
        for($i=0;$i<count($board);$i++){
            for($j=0;$j<count($board[$i]);$j++){
                //先过滤一遍边界
                if($i==0 || $j==0 || $i==count($board)-1 || $j==count($board[$i])-1){  
                    //在判断当前边界的值是否是O,递归处理所有的边界
                    if($board[$i][$j]=='O'){
                        $this->helper($board,$i,$j);
                    }
                }

            }
        }
        
        //这次遍历是为了把剩下被包围的O转为成X，之前边界转换的中间值Y重新转换为O,证明他没被包围还活着
        for($i=0;$i<count($board);$i++){
            for($j=0;$j<count($board[$i]);$j++){
                
                if($board[$i][$j]=='O'){
                    $board[$i][$j]='X';  
                }
                 if($board[$i][$j]=='Y'){
                    $board[$i][$j]='O';
                }
        }
    }
        return $board;
  }
    
    function helper(&$board,$i,$j){
        if($board[$i][$j]=='O'){
            $board[$i][$j]='Y';
            if($i>0 && $board[$i-1][$j]=='O'){
                $this->helper($board,$i-1,$j);
            }
            if($j<count($board[$i])-1 && $board[$i][$j+1]=='O'){
                $this->helper($board,$i,$j+1);
            }
            if($i<count($board)-1 && $board[$i+1][$j]=='O'){
                $this->helper($board,$i+1,$j);
            }
            if($j>0 && $board[$i][$j-1]=='O'){
                $this->helper($board,$i,$j-1);
            }
        }
    }
}