Leetcode动态规划之PHP解析(70. Climbing Stairs)
2019-5-15 星期四 开始吧
动态规划题第一天
题目描述
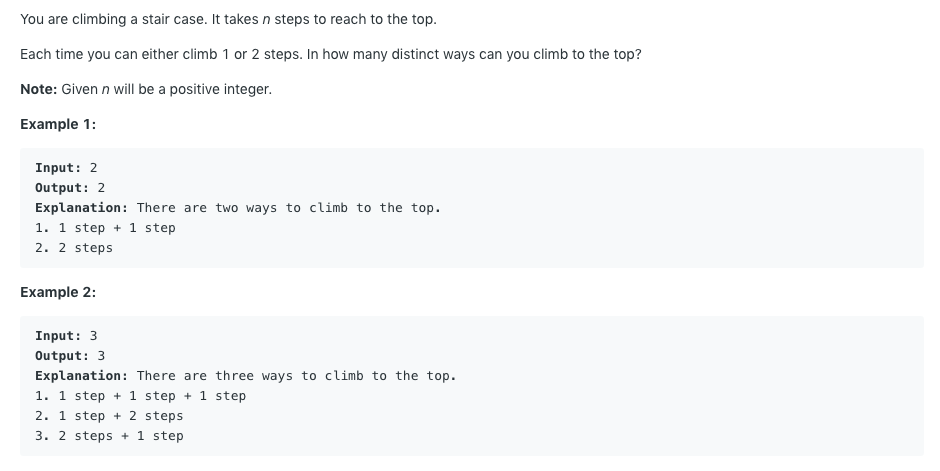
这是一个爬楼梯的问题,给定一个数字代表着楼梯的层数,每次你可以走一步或者两步,求最终你可以有几种方式到达顶峰。
看了一个专栏提到,关于解动态规划的题目可以从以下几点入手。
1.递归+记忆化 ->反向推出递推公式。
2.状态的定义 opt[n],dp[n].
3.状态转移的方程dp[n]=dp[n-1]+dp[n-2]
4.最优子结构
题目分析
我们先用回溯法的思想来解,第n层台阶总的走法就等于它相邻台阶总走法+两阶台阶之外的走法,得出的递推公式.
f(n)=f(n-1)+f(n-2)
所以代码可以直接写出。
/**
* @param Integer $n
* @return Integer
*/
function climbStairs($n) {
if($n<=1){
return 1;
}
return $this->climbStairs($n-1)+$this->climbStairs($n-2);
}
但是这种递归的话进行了大量重复的运算,我们来看php的运行结果。你可以看到,当n等于44的时候运算超时了。

动态规划
动态规划最重要的两点就是状态的定义(有点飘)和递推的方程(递推公式很难推,学动态规划需要去大量的实战练习)。
f[n]=f[n-1]+f[n-2]
递推方程就是一个斐波那契数列
/**
* @param Integer $n
* @return Integer
*/
function climbStairs($n) {
if($n<=1){
return 1;
}
$res[0]=1;
$res[1]=1;
for($i=2;$i<=$n;$i++){
$res[$i]=$res[$i-1]+$res[$i-2];
}
return $res[$n];
}
Github整理地址:https://github.com/wuqinqiang/leetcode-php


No Comments